{Решение дифференциального уравнения
первого порядка y'=f(x,y) методом Рунге-Кутта
Дьяконов В.П. MathCad}

[koef ax=x ay=y func k1=h*f
      ax=x+h/2 ay=y+k1/2 func k2=h*f
      ax=x+h/2 ay=y+k2/2 func k3=h*f
      ax=x+h ay=y+k3 func k4=h*f
      k=k1+2*k2+2*k3+k4]

[PA koef x=x+h y=y+k/6 z=exp(x^2/2){проверка}]

[func f=ax*ay]
x=0 y=1 h=0.1

PA x=? y=? z=?
PA x=? y=? z=?
PA x=? y=? z=?
PA x=? y=? z=?
PA x=? y=? z=?
PA x=? y=? z=?
PA x=? y=? z=?
PA x=? y=? z=?
PA x=? y=? z=?
PA x=? y=? z=?

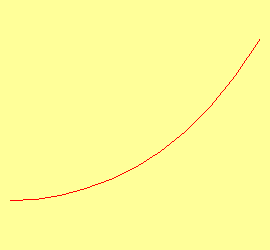
{Построим график синим цветом}
win(270,250,255,255,200)
[GA xx=250*x+10 yy=450-250*y PA]
x=0 y=1
pen(1,0,0,255)
graph(GA,xx,yy,t,0,9,1)

{Сверху нарисуем график точного решения
красным цветом}
[PA x=h*t y=exp(x^2/2)]
x=0 y=1
pen(1,255,0,0)
graph(GA,xx,yy,t,0,10,1)

 Результат:

 Решение дифференциального уравнения
первого порядка y'=f(x,y) методом Рунге-Кутта
Дьяконов В.П. MathCad 

[koef ax=x ay=y func k1=h*f
      ax=x+h/2 ay=y+k1/2 func k2=h*f
      ax=x+h/2 ay=y+k2/2 func k3=h*f
      ax=x+h ay=y+k3 func k4=h*f
      k=k1+2*k2+2*k3+k4]

[PA koef x=x+h y=y+k/6 z=exp(x^2/2){проверка}]

[func f=ax*ay]
x=0 y=1 h=0.1

PA x=0.100000 y=1.005013 z=1.005013
PA x=0.200000 y=1.020201 z=1.020201
PA x=0.300000 y=1.046028 z=1.046028
PA x=0.400000 y=1.083287 z=1.083287
PA x=0.500000 y=1.133148 z=1.133148
PA x=0.600000 y=1.197217 z=1.197217
PA x=0.700000 y=1.277621 z=1.277621
PA x=0.800000 y=1.377128 z=1.377128
PA x=0.900000 y=1.499302 z=1.499303
PA x=1.000000 y=1.648721 z=1.648721

 Построим график синим цветом 
win(270,250,255,255,200)
[GA xx=250*x+10 yy=450-250*y PA]
x=0 y=1
pen(1,0,0,255)
graph(GA,xx,yy,t,0,9,1)

 Сверху нарисуем график точного решения
красным цветом 
[PA x=h*t y=exp(x^2/2)]
x=0 y=1
pen(1,255,0,0)
graph(GA,xx,yy,t,0,10,1)